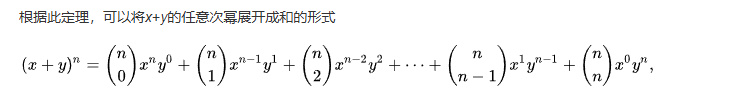总结为掉分,掉得不应该。
教训是下次多读几遍题目,知道题目要做什么
A
汉明码,直接找不同
B
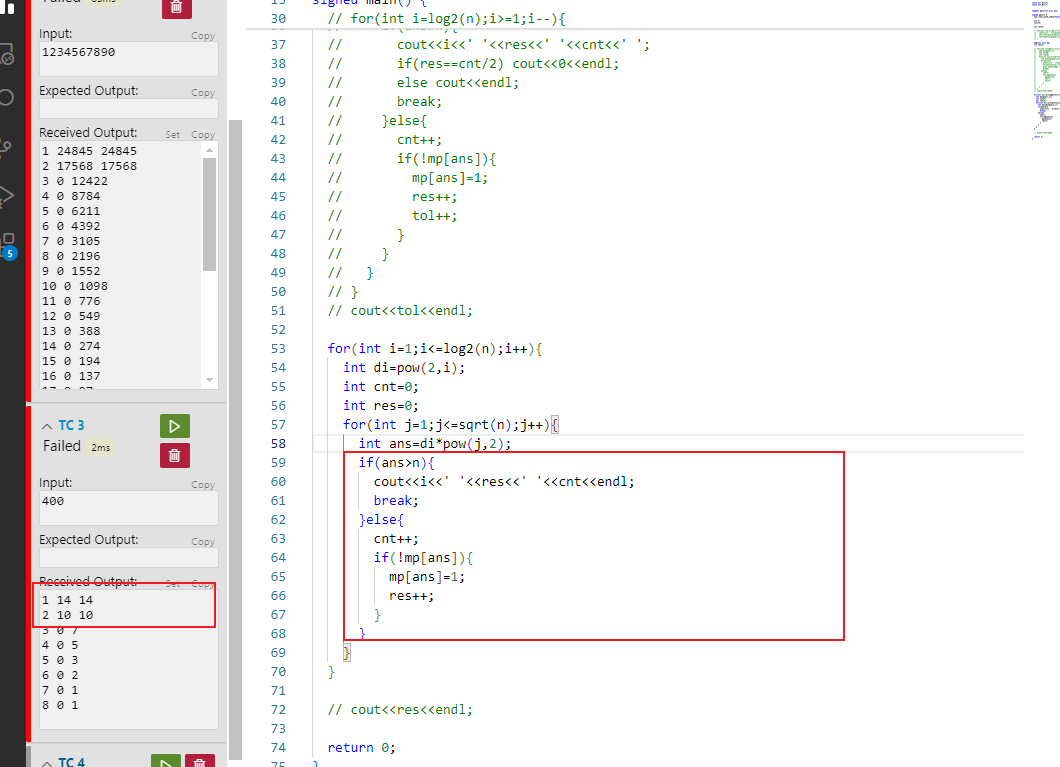
给数字排序,打得有点繁琐了
C
并查集,打得也是有点繁琐。
重要思想:在并查集的一开始,把每一个看成一个连通块,每连接一条边,连通块就减少一个。
总结:相应的,最后用总点数减去剩下的连通块,就是连的边数
D
一开始直接看样例,没有懂样例的最后一个例子,本人也因没认真读懂题目,一直在找最小换座位次数。
题意:找到第一次出现和第二次出现都相邻的点对数
方法:开一个数组维护一个数第一次出现的位置,当数x第一次出现的位置,和x前一位数 y ,当且仅当 x和y第一次出现的位置相差1的时候才有统计答案。特殊地,(1) 如果y前一个位置的是他自己第一次出现的位置,这个时候的不能统计; (2) 如果刚统计完就是自己也不能统计;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
| #include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
void solve(){
int n;
cin>>n;
vector<int> a(2*n+2);
for(int i=1;i<=2*n;i++) cin>>a[i];
int cnt=0;
vector<int> yi(n+1);
for(int i=1;i<=2*n;i++){
if(yi[a[i]]&&yi[a[i-1]]&&a[i-1]!=a[i]){
if(yi[a[i-1]]==i-1) continue;
if(i-1-yi[a[i-1]]==1) continue;
if(abs(yi[a[i]]-yi[a[i-1]])==1){
cnt++;
}
}
if(!yi[a[i]]){
yi[a[i]]=i;
}
}
cout<<cnt<<endl;
}
signed main() {
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int t;
cin>>t;
while(t--){
solve();
}
return 0;
}
|
F
感觉可以用二项式展开定理

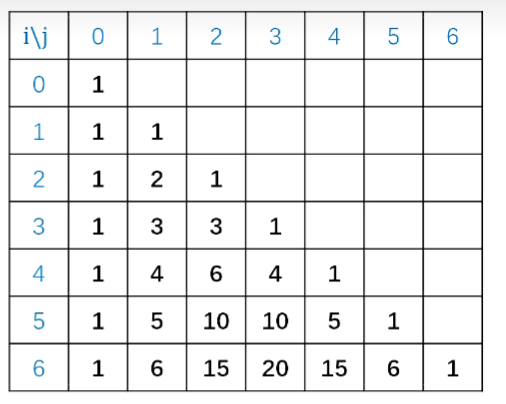
知识铺垫
- 求组合数
递推法
递推公式:
含义:从n个不同的书中选出m个的方案数,对于第一个数有 选或 不选 两种决策,如果选,则从剩下的 n-1 个中选 m-1 个,如果不选,则从剩下的 n-1 个中选 m 个
示意图: 来自左上和上方

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| #include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
const int N=110;
int C[N][N];
const int mod=1e9+7;
signed main() {
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int n;
cin>>n;
for(int i=0;i<=n;i++){
for(int j=0;j<=i;j++){
if(j==0) C[i][j]=1;
else C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
}
}
return 0;
}
|
- 快速幂 + 组合公式
板子,用于大幂摸与乘法逆元
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| #include<bits/stdc++.h>
using namespace std;
#define int long long
typedef pair<int,int> pii;
int qui(int a,int k,int p){
int res=1;
while(k){
if(k&1) res=res*a%p;
k>>=1;
a=a*a%p;
}
return res;
}
const int N=1e5+10;
int f[N],g[N];
const int mod=1e9+7;
signed main() {
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int n,m;
cin>>n>>m;
g[0]=f[0]=1;
for(int i=1;i<=n;i++){
f[i]=f[i-1]*i%mod;
g[i]=g[i-1]*qui(i,mod-2,mod)%mod;
}
cout<< f[n]*g[m]%mod*g[n-m]%mod;
return 0;
}
|
- 卢卡斯定理
待写…….
解决问题
题意:
思路:用组合意义取k次幂,二项式定理。
类似:NOI2009管道取珠
思路@wjh
以第i个元素结尾的子数组和
每增加一个元素会产生什么影响
请观察如下式子:
下列每个元素 表示从下标 到 的子数组的和,以 为例
观察上式我们可以思考:
从第二层开始,当前层能否由上一层得来,由此,我们对式子进行变形:
我们继续思考对每个元素计算k次方,当前层会比上一层多出什么:
以第4层作为当前层(第4个元素结尾构成的子数组和有四种):
发现第四层比第三层多了一项[4,4]不好整体转移
第4个元素结尾构成的子数组和的==k次幂==有四种:
我们先不看
以第4层作为当前层
令上一层子数组和的==k次幂==的 和为 ;
令当前层子数组和的==k次幂==的 和为 ;
由二项式展开定理,我们可以得到:
我们以i元素结尾的所有子数组和的k次幂的和作为状态:
状态转移方程可以写成如下:
上一个引用块的第3步用到了二项式展开定理,因此在代码中体现为多了m这种循环
这个式子意味着需要保留以第i个元素结尾的子数组和的1到k次幂的和的状态。
具体如下:
也就是:
是被提前算出来的 b1[0]
是被提前算出来的 b1[1]
是被提前算出来的 b1[2]
也就是以第三个元素结尾的子数组的和的1-2次幂 分别和 的2-1次幂相乘
也就是:
在代码中体现为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
| #include<bits/stdc++.h>
using namespace std;
typedef pair<int,int> pii;
#define int long long
const int N=2e5+10,M=11;
const int mod=998244353;
int a[N],ap[N];
int c[M][M];
int dp[N][M];
signed main() {
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
int n,k=10;
cin>>n>>k;
for(int i=1;i<=n;i++){
cin>>a[i];
a[i]%=mod;
}
for(int i=0;i<=k;i++){
for(int j=0;j<=i;j++){
if(j==0) c[i][j]=1;
else c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
}
int res=0;
for(int i=1;i<=n;i++){
ap[0]=1;
for(int j=1;j<=k;j++){
ap[j]=ap[j-1]*a[i]%mod;
}
for(int j=0;j<=k;j++){
int sum=0;
for(int m=0;m<=j;m++){
int x=c[j][m]%mod;
x=(x*dp[i-1][m])%mod;
x=(x*ap[j-m])%mod;
sum=(sum+x)%mod;
}
dp[i][j]=(sum+ap[j])%mod;
}
res=(res+dp[i][k])%mod;
}
cout<<res<<endl;
return 0;
}
|